给我一个支点，我能撬动整个地球。

                            ——阿基米德

文首这句豪迈的宣言出自希腊化时代颇负盛名的数学家、物理学家、发明家、工程师、天文学家阿基米德，其中蕴含的是物理学中的杠杆原理。只要有合适的支点与杠杆，即使力量微小也能撼动极重的物体。

我们可以先来感受一下当“大力士”的感觉。湖北省科技馆数理世界展厅中的这件展品——巨大杠杆，正是利用杠杆原理，让人能够轻松拉动汽车。

那什么是杠杆呢？通俗来讲，杠杆是一根绕着固定的支撑点旋转的硬棒。生活中许多常见的简易机械其实都是杠杆，小区游乐场里的跷跷板，工具箱里的撬棍，在实际使用中都可以看作是一根杠杆。

人们对杠杆的应用可以追溯到旧石器时代晚期，那时已经出现了一种简易装置——投矛器，利用杠杆原理提高矛的投掷距离、打击力量和准确性，即使是纤弱的人类也能借助智慧弥补体力与力量的不足，在狩猎中洞穿野兽的皮毛。中国的战国时期，《墨子》一书中已有对杠杆平衡的几种条件的描述。早在春秋时期，就已经出现了“桔槔”（俗称“吊杆”）这种原始的提水工具。

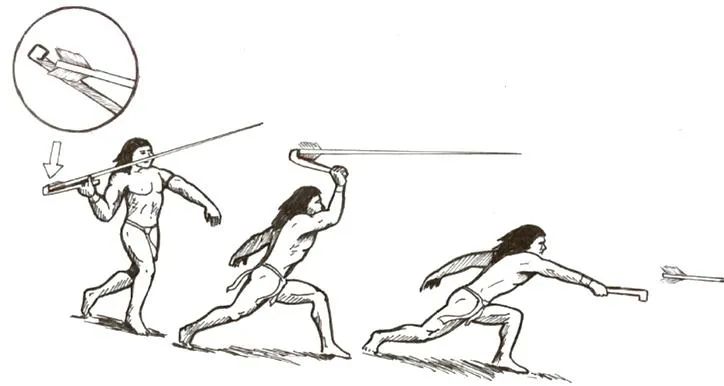
投枪器是一种利用杠杆原理来增加投枪的初速度的工具。其中一端有钩状的支撑物来固定住投枪的尾端，使用者通常以一手抓住没有杓状或钩状物的那一端，以上臂和腕作动作将标枪投出。

桔槔是在一根竖立的架子上加上一根细长的杠杆，当中是支点，末端悬挂重物，前段悬挂水桶。当人把水桶放入水中打满水以后，由于杠杆末端的重力作用，便能轻易把水提拉至所需处。

杠杆的应用有着悠久的历史，人们在日常生活中大量应用这种简易机械，却并未精确简洁地概括杠杆的平衡条件，直到阿基米德推导出杠杆原理。在《论平面图形的平衡》一书中，阿基米德从杠杆的实际应用出发，将杠杆应用中的经验知识作为一种“公理”，然后运用几何学进行严密的逻辑验证，得出结论：二重物平衡时，它们离支点的距离与重量成反比（当杠杆处于静力平衡时，其动力乘以动力臂等于阻力乘以阻力臂）。用公式表示为：

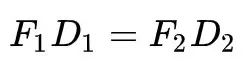
我们可以用一张简化的图片来表示杠杆原理中的几大要素：

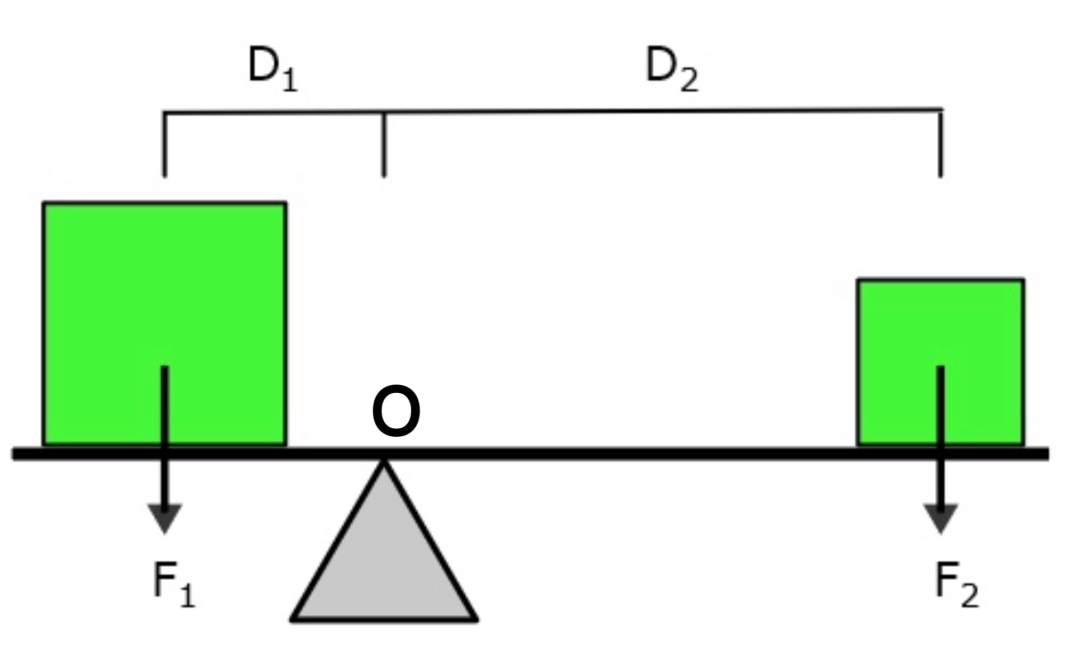
支点：杠杆绕着转动的点，通常用字母O来表示。

动力：使杠杆转动的力，通常用F1来表示。

阻力：阻碍杠杆转动的力，通常用F2来表示。

动力臂：从支点到动力作用线的距离，通常用D1表示。

阻力臂：从支点到阻力作用线的距离，通常用D2表示。

公元前3世纪末，罗马共和国与迦太基为争夺西西里岛的霸权而开战，史称布匿战争。阿基米德根据杠杆原理进行了一系列发明创造，在抵抗罗马人的过程中发挥出巨大作用。据说，阿基米德制造出能够射出飞弹和巨石的投石器将罗马人挡在城外。连罗马的将军马克卢斯也发出感叹：“这是场罗马舰队与阿基米德一人的战争”、“阿基米德简直是神话中的百手巨人”。

法国莱博德城堡的重力抛石机

阿基米德用到的投石器是一种省力杠杆，主要特点是动力臂长于阻力臂，以达到省力的效果。生活中常见的省力杠杆还有开瓶器、取钉器等物品。

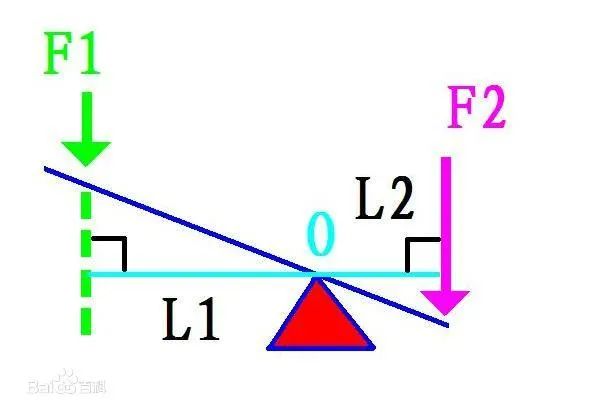
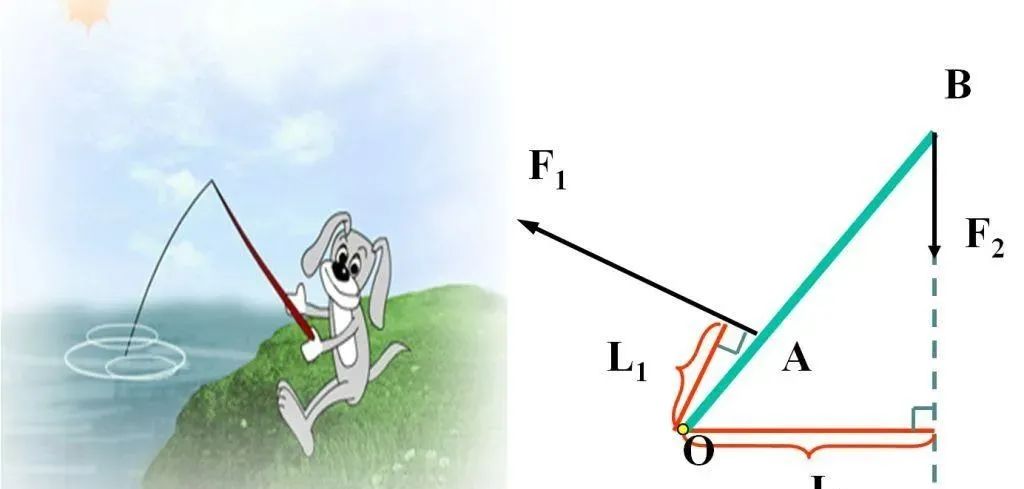
与省力杠杆相反的是费力杠杆，动力臂比阻力臂短。费力杠杆虽然不能省力，但可以节省动力移动的距离。日常生活中典型的利用费力杠杆的场景大概就是钓鱼了。

从动图可以看出这个费力杠杆是真的很费力了。图源网络

此外还有一种等臂杠杆，动力臂与阻力臂相等，既不省力，也不节省距离，如天平与跷跷板。

当我们看向本文开头，阿基米德撬动地球的话好像在理论上是真的可行的，那实际上是否可行呢？

假定地球是静止的，地球的质量约为5.965×10²⁴kg，为方便计算，我们将质量取为6×10²⁴kg，将支点放在与地球相近的月球上，并且假定月球也是静止的，已知地月距离是384400km，根据杠杆原理计算，我们只需要一根一千万亿光年长的杠杆就可以撬动地球了！

奇奇怪怪的知识又增加了呢。